Adriana Sanchez Hidalgo: mayo 2011

domingo, 22 de mayo de 2011

3.16 Propiedades de La Transformada Inversa

Propiedades de La Transformada Inversa de Laplace
Propiedad de linealidad
Teorema. Si c1 & c2 son constantes arbitrarias y f1(s) & f2(s) son las transformadas de Laplace de F1(t) & F2(t) respectivamente, entonces:

Primera propiedad de traslación

Segunda propiedad de Traslación
Propiedad del cambio de escala.
Transformada inversa de Laplace de las Derivadas.

3.15 Algunas Tranformadas Inversas

Ejemplo 1

Calcular la Transformada de Laplace
$\mathcal{L}^{-1}{\frac{s}{(s^2 + 4)}}$

Puesto que

$\mathcal{L}\{Cos(2t)\}= \frac{s}{s^2+4}$

por lo tanto tenemos que:

$\mathcal{L}^{-1}{{\frac{s}{s^2 + 4}}= {Cos(2t)}$

Ejemplo 2

Determinar $\mathcal{L}^{-1}{{\frac{3s-1}{s^2+4}}$

$\mathcal{L}^{-1}{{\frac{3s}{s^2+4}}+{{\frac{-1}{s^2+4}}$

$3\mathcal{L}^{-1}{{\frac{s}{s^2+4}} - \mathcal{L}^{-1}{{\frac{1}{s^2+4}}$

Utilizando las transformaciones de la Tabla1 obtenemos: $\mathcal{L}^{-1}{{\frac{3s-1}{s^2+4}}=3cos(2t)-{{\frac{1}{2}sen(2t)}$

Ejemplo 3

Determinar $\mathcal{L}^{-1}\left\{{{\frac{3s+5}{s^{2}+7}}}\right\}}$

$\mathcal{L}^{-1}\left\{{{\frac{3s}{s^{2}+7}+\frac{5}{s^{2}+7}}}\right\}$

$f(t) = 3 \cos{\sqrt[]{7}t}+ 5 \sin{\sqrt[]{7}t$

Ejemplo 4

Determinar $\mathcal{L}^{-1}\left\{{\frac{1}{(s-1)(s+2)(s+4)}}\right\}$

Por fracciones parciales..... $\frac{A}{s-1}+\frac{B}{s+2}+\frac{C}{s+4}= \frac{1}{(s-1)(s+2)(s+4)}$

$A=\frac{1}{15}$ $B = \frac{-1}{3}$ $C = \frac{1}{10}$

$\mathcal{L}^{-1}\left\{{\frac{\frac{1}{15}}{s-1}-\frac{\frac{1}{3}}{s+2}+\frac{\frac{1}{10}}{s+4}}\right\}$

$f(t) = \frac{1}{15}e^{t}-\frac{1}{3}e^{-2t}+\frac{1}{10}e^{-4t}$

Ejemplo 5

Determinar $\mathcal{L}^{-1}\left\{{\frac{1}{s^7}}\right\}$
$\mathcal{L}^{-1}\left\{{\frac{6!}{6! s^7}}\right\}$
$=\frac{1}{6!}\mathcal{L}^{-1}\left\{{\frac{6!}{ s^7}}\right\}$
$=\frac{1}{6!}t^6$

Ejemplo 6

Determinar $\mathcal{L}^{-1}\left\{{\frac{k}{s}}\right\}$

Dado que $\mathcal{L}\left\{{k}\right\} = \frac{k}{s}$

obtenemos que $\mathcal{L}^{-1}\left\{{\frac{k}{s}}\right\} = k$

miércoles, 18 de mayo de 2011

3.14 Transformada Inversa

La transformada inversa de Laplace

Al aplicar la transformada de Laplace a una ecuación diferencial la convertimos en una ecuación algebraica, la cual podemos resolver para

, es decir,

. Ahora, como ${\cal L} \{y(t) \} = Y(s)$ si pudiéramos devolvernos obtendríamos la solución

que buscamos. Es decir, necesitamos de la transformada inversa ${\cal L}^{-1} \{Y(s) \}$ , para hallar la función

$\displaystyle y(t) = {\cal L}^{-1} \{F(s) \} = {\cal L}^{-1} \{ G(s) \}$

3.13 Tranformada de Laplace de la Función Delta-Dirac

La transformada de Laplace no es más que otra técnica para la resolución de ecuaciones diferenciales. Sin embargo, su popularidad (sobre todo en problemas de ingeniería) radica en que nos permite resolver ecuaciones en las cuales el término independiente puede ser sumamente "mal portado". En el caso de la ecuación (3), el término H(t) podría no ser una función continua (lo cual representa mejor a la realidad), con lo cual la función x (t) sería diferenciable por pedazos. El tipo de funciones H(t) que vamos a analizar son funciones que son nulas, excepto en algunos intervalos o instantes de tiempo predeterminados.

La función más simple de este tipo es la función escalón o función de Heaviside. Ésta se define para cualquier a = 0 como sigue:

Es fácil ver que su transformada de Laplace está dada por

Una variante de esta función es la siguiente:

Asimismo, tomando el límite cuando .t. 0 se define

A esta última función se la conoce como la función delta de Dirac. Llamamos función de impulso a cualquier función que se obtenga como una combinación lineal de deltas de Dirac.

Las funciones descritas arriba se ilustran en la figura 1.

Figura 1: Aquí se ilustran las funciones y = ua (t), y = u.t, a (t) y äa (t).

Intuitivamente, äa(t) es una función nula excepto en t = a, punto para el cual toma un valor "infinito". Podemos imaginar que esta función representa un shock o impulso en t = a, algo así como un martillazo, una descarga eléctrica o, porque no, una ganancia o pérdida inesperada de capital representada por un instante de inversión "infinita". A pesar de que parece absurdo, desde el punto de vista matemático, definir a la función de Dirac, la aplicación de la transformada de Laplace la convierte en una función manejable como vemos a continuación.

Proposición 3.1 La transformada de Laplace de äa(t) está dada por

Demostración

Dados a = 0 y .t > 0, calculemos primero L [u.t,a(t)](s) como sigue:

Asimismo, tenemos que

con lo cual se concluye la demostración. ¥

Observemos que tiene sentido poner

domingo, 15 de mayo de 2011

3.12 Función de Delta-Dirac

La delta de Dirac (inapropiadamente llamada función delta de Dirac) es una distribución (función generalizada) introducida por primera vez por el físico inglés Paul Dirac, en tanto que distribución define un funcional en forma de integral sobre un cierto espacio de funciones.

Los sistemas mecánicos trabajan muchas veces bajo una fuerza externa de magnitud mayor que actúa sólo durante un periodo muy corto. Por ejemplo, un relámpago puede hacer vibrar el ala de un avión, o una masa sujeta a un resorte puede recibir un fuerte impacto con la cabeza de un martillo, una pelota puede lanzarse hacia las alturas por un golpe violento dado con algún tipo de palo. Por tanto estos fenómenos se comportan de la manera que en un intervalo mínimo de tiempo experimentan fuerzas muy grandes y a su vez esta fuerza se disipa instantáneamente.

3.11 Transformada de Laplace de 1era Función Periódica

Una función Periódica es una función que se repite. El período de la función es el mínimo intervalo de tiempo donde la función no se repite.
Matemáticamente una función es periódica con período T es una función f(t) que cumple:

Dicho en términos simples, lo que es o pasa con la función en el intervalo describe o determina totalmente a la función.
Gráficamente una función periódica queda

3.10 Teorema de Convulcion

En matemática, el teorema de convolución establece que bajo determinadas circunstancias, la Transformada de Fourier de una convolución es el producto punto a punto de las transformadas. En otras palabras, la convolución en un dominio (por ejemplo el dominio temporal) es equivalente al producto punto a punto en el otro dominio (es decir dominio espectral).

Sean

f

g

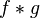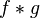dos funciones cuya convolución se expresa con $f \ast g$ . (notar que el asterisco denota convolución en este contexto, y no multiplicación; a veces es utilizado también el símbolo $\otimes$ ). Sea $\mathcal{F}$ el operador de la transformada de Fourier, con lo que $\mathcal{F}[f]$ y $\mathcal{F}[g]$ son las transformadas de Fourier de f y g, respectivamente.

Entonces

$\mathcal{F}[f*g]=\sqrt{2\pi} (\mathcal{F}[f]) \cdot (\mathcal{F}[g])$

donde · indica producto punto. También puede afirmarse que:

$\mathcal{F}[f \cdot g]=\frac{\mathcal{F}[f]*\mathcal{F}[g]}{\sqrt{2\pi}}$

Aplicando la transformada inversa de Fourier $\mathcal{F}^{-1}$ , podemos escribir:

$f*g=\sqrt{2\pi} \mathcal{F}^{-1}[\mathcal{F}[f]\cdot\mathcal{F}[g]]$